
Algo 4: (1,1,x) w/ H or V Nearest Neighbors
Trouble arises when the EM algorithms, described from a physics point
of view here,
are transformed into pipelinable VHDL.
Most implementations of the algorithm either miss clear LMs,
find spurious LMs or mis-assign energy to LMs that are found. (Some
examples are given below.)
The best algorithm we have found so far is rather different in structure from the "physics algorithm" but should return essentially the same results. It consists of the following steps, most of which are done in parallel in the firmware.
| 0 | if this point is not a surviving LM |
| Et(H) | if Et(H-ROI) >= Et(V-ROI) at this point |
| Et(V) | if Et(V-ROI) > Et(H-ROI) at this point |
Detailed Documentation |
pdf | doc |
Pathologies |
none found so far |
Algo 0: Basic Algorithm
The starting point of the basic pipelinable algorithm involves
constructing
parallel grids of Horizontal and Vertical ROI sums as
shown below:
| Horizontal: | Vertical: |
 |
 |
Local Maximum finding is done in parallel on both the H and V ROI grids. The criteria for finding a LM by comparing with the 8 surrounding ROIs (2,0,1 algorithm) is shown below. To be considered as a local maximum, the central ROI (S) must be > or >= to the 8 ROIs surrounding it depending on position.
ROI-based LM Finding:
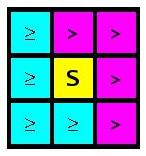
The Et chosen at each point on the output grid is then:
| 0 | if this point is not a LM |
| Et(H) | if Et(H-ROI) >= Et(V-ROI) at this point |
| Et(V) | if Et(V-ROI) > Et(H-ROI) at this point |
Algo 1.b: H+V Sum Algorithm (07-Apr-05)
This variant of the EM algorithm gets around some of the problems
shown below by effectively giving more weight to the lower-left anchor
of the H- and V-ROIs. This is accomplished by simply summing the H-ROI
and V-ROI associated with a given grid position and using the H+V sum
grid as the basis for LM finding.
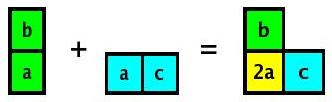
If a LM is found, the Et output for that position is chose according
to the rule above:
| 0 | if this point is not a LM |
| Et(H) | if Et(H-ROI) >= Et(V-ROI) at this point |
| Et(V) | if Et(V-ROI) > Et(H-ROI) at this point |
| No. | TT input | Et output | Comments | ||||||
| 1 |
|
|
details fails for Et(left) <= Et(right)/2 |
||||||
|
|
details works fine ! |
|||||||
|
|
details works fine ! |
Algo 2.c: Validate H-LM w/ V-ROIs (06-Apr-05)
This algorithm gets around the problems seen in
Algo 3.a by adding compares to V-ROIs when
searching for LMs in the H-ROI grid and vice versa, as shown below.
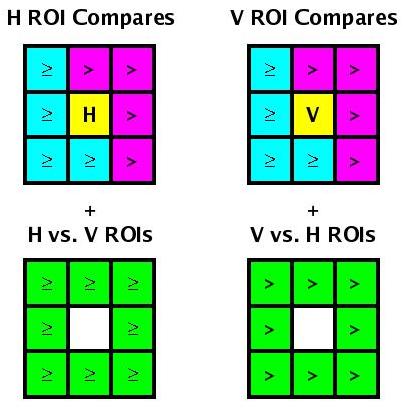
| No. | TT input | Et output | Comments | ||||||
| 1 |
|
|
details fails for Et(left) <= Et(right) |
||||||
|
|
details works fine ! |
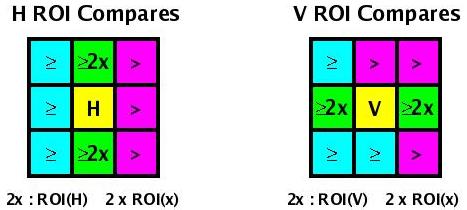
Algo 3.a: Isolated H- and V-LMs (05-Apr-05)
The compares done on the H-ROI and V-ROI grids are modified to include
an isolation ratio (set to 2 in the diagram below) that
requires potential LMs to have significantly greater Et than several
cells near them. The orientation of the cells that must pass the
isolation test is chosen to kill spurious clusters produced by the
base algorithm.
| No. | TT input | Et output | Comments | ||||||||
| 1 |
|
|
details |
Algo 3.b: Different Isolation Scheme (07-Apr-05)
This is an modification of Algo 3.a that adds
a veto on any LM that has other LMs near it as shown below:

| No. | TT input | Et output | Comments | ||||||
| 1 |
|
|
details | ||||||
|
|
details works fine ! |
|||||||
|
|
details works fine ! |