DØ Run IIb L1Cal Tau Algorithm
updated: 28-Jul-05
Index
-
Description of the Algorithm
-
Divides in the Firmware
Algorithm Description
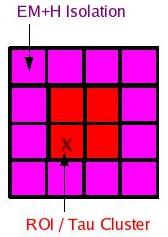
The tau algorithm is based on the results of LM-finding used for the
Jet algorithm.
Two quantities are calculated:
- Et(2x2):
the sum of TT Et's in the 2x2 ROI used for Jet LM-finding
- Isolation:
Et(2x2)/Et(4x4)
Et(2x2) - pedestal subtracted,
encoded into a 3-bit word corresponding to the highest of 7
Et thresholds passed,
is reported as the Et of the Tau Object if:
- the ROI is found as a LM
- Isolation > cut
Implementation of Divides in the Firmware
Steps in the algorithm from Jaro Ban
-
Form Et sums - both are 12-bit integers
- Et(2x2) = numer(11..0)
- Et(4x4) = denom(11..0)
-
Perform the ratio numer(11..0)/denom(11..0)
for denom() >= numer()
with result do(7..0)
Note: result varies from 0 to 256/512 with 8 bit precision
over the dynamic range 256/1; This is relevant for you to know.
The divide operation itself has a few steps. Among them are:
- normalize denom (find the leading one)
- produce 1/(denom(11..0)) through the lookup table
- multiply numer * (1/denom) by hardware
(integer) multiplier
- renormalize the result (do)
-
Because the pedestals are subtracted,
(and we will have the noise in the data)
the final ratio result is defined as:
| Ped
Subtracted |
|
| Et(2x2) |
Et(4x4) |
8-bit Ratio |
| negative | negative | 00000000 |
| negative | positive | 00000000 |
| positive | negative | 11111111 |
| positive | positive | do |
This operation is performed in parallel with the divide operation.
-
At the end of this architecture we have a lookup table which forms
final 3 bits of the ratio. Input to the lookup table is the ratio
produced as described in the step above. The content of the lookup
table is (user) defined by someone who wants to do the cuts on the
ratio. At the moment lookup table simply reproduces (puts to the
output) highest 3 bits of the ratio.
